# Версоры

[Кватернионы](./quaternion-rus.md) - это гиперкомплексные числа, у которых имеется одна действительная компонента и три мнимых компоненты:

![Формулы определяющие кватернион](./media/quaternion_definition.png)

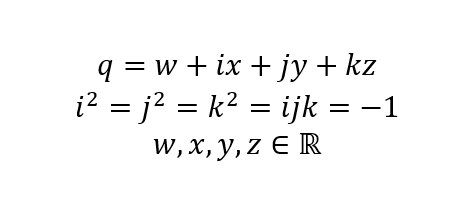
    q = w + ix + jy + kz
    i<sup>2</sup> = j<sup>2</sup> = k<sup>2</sup> = -1

Кватернионы были открыты математиком Уильямом Гамильтоном и представлены публике в 1843 году.

Вское Уильям Гамильтон предложил особый класс кватернионов, которые назвал версорами.

Версор - это кватернион, модуль которого равен единице. То есть, к формулам, определяющим квартернионы, необходимо добавить услвие, что модуль кватериона равен единице.

![Формулы определяющие версор](./media/versor_definition.png)

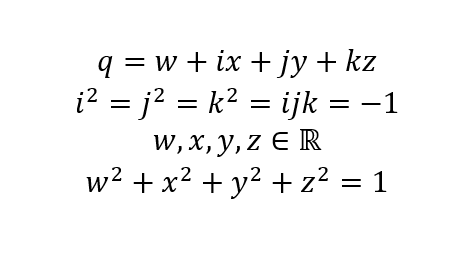
Название происходит от латинского глагола "versare", означаюшего "поворачивать", "вращать", к которому добавлено латнское окончание -or, которое обозначает субъект, выполняющий действие.

Дословно латинское слово "versor" можно перевести как "вращатель" или "поворачиватель". 

Версоры оказались довольно хорошим инструментом для описания поворотов в трёхмерном пространстве.

Для комбинации двух последовательных поворотов оказалось полезной операция умножения кватернионов, а для получения обратного поворота - операция получения сопряжённого кватерниона.

При умножении двух версоров (кватернионов единичной длины) и при взятии сопряжённого версора результат также будет версором, то есть кватернионом единичной длины.

Сложение и вычитание двух кватернионов, а также умножение и деление кватерниона на число оказались не нужны для описания поворотов в трёхмерном пространстве.

Несмотря на то, что версоры как класс кватернионов были предложены ещё Уильямом Гамильтоном для описаний поворотов ещё в середине 19 века, в русскоязычной литературе термин "версор" встречается настолько редко, что можно сказать, что не употребляется.

## Преимущества версоров над кватернионами

Главным преимуществом выделения версоров как отдельной от кватернионов абстрации заключается в том, что версоры сохраняют модуль равный единице, то есть, версоры не вырождаются.

Кватернионы, модуль которых не равен единице в результате множества операций умножения могут дать кватернион, модуль которого может оказаться настолко близок к нулю, что будет сопоставим с величиной погрешности.

На практике модуль версора не всегда равен единице, но близок к единице из-за наличия погрешности типов **float** и **double** (**binary32** и **binary64**). Но функции библиотеки BGC обеспечивают, чтобы модуль веросра, полученного в результате некоторой операции, не отколнялся от единицы на величину не превышающую заданную погрешность.

И это является вторым преимуществом применения именно версоров для описания поворотов. Разработчику, который использует библиотеку, не нужно производить нормализацию, как это пришлось бы делать с обычными кватернионами.

Но функции библиотеки не всегда производят нормализацию версоров, а только тогда, когда это необходимо. Функции библиотеки нормализуют полученный версор только тогда, когда модуль версора отклоняется от единицы больше, чем на предопределенную величину погрешности (эпсилон).

В большинстве случаев, когда входные параметры являются версорами (нормализованными кватернионами), модуль полученного версора также не сильно отклоняется от единицы, а потому нет необходимости производить нормализацию. Таким образом, можно избежать трудоемких операций, таких как вычисление квадратных корней и деление. Такой подход позволяет повысить производительность и поддерживать версоры нормализованными.

## Версоры в библиотеке

Библиотека имеет отдельную реализацию для версоров в виде специальных структур и набора функций, которые поддерживают модуль версоров близким к единице, посольку необходимо поддерживать модуль веросоров близким к единице, а также версорам не нужны сложение и вычитание, а также умножение и деление на число.

Для описания версора имеется две структуры:

    typedef struct {
        const float s0, x1, x2, x3;
    } BgcVersorFP32;

    typedef struct {
        const double s0, x1, x2, x3;
    } BgcVersorFP64;

Поле **s0** вещественной частю версора (нормализованного кватерниона), а поля **x1**,  **x2** и  **x3** являются мнимыми компонентами версора.

Поля структур намеренно объявлены констрантными (const), чтобы побудить разработчика использовать функции работы с версорами, вместо того, чтобы непосредственно задавать значения полей. Функции отвечающие за операции над версорами поддерживают модуль полученных версоров равным единице.

С данными структурами лучше использовать специальные функции, которые позволяют устанавливать новые значения в поля структур **BgcVersorFP32** и **BgcVersorFP64**.

## Операции с версорами

- [Сброс состояния (reset)](./versor-reset-rus.md)
- [Указание значений компонент (set values)](./versor-set-values-rus.md)
- Копирование значений компонент (copy)
- Обмен значений компонент (swap)
- Построение на основе поворота (set turn)
- Проверка на отсутствие поворота (is idle)
- Преобразование типа (convert)
- Сокращение поворота (shorten)
- Инверсия (invert)
- Комбинирование (combine)
- Получение описание поворота (get rotation)
- Получение матрицы поворота (get rotation matrix)
- Получение матрицы обратного поворота (get reverse matrix)
- Поворот вектора (turn vector)
- Обратный поворот вектора (turn vector back)
- Сравнение (are close)